Heinz Schumann
Geometrische Extremwertaufgaben in dynamischer Behandlung
| “Da die Einrichtung der ganzen Welt die vorzüglichste ist, und da sie vom weisesten Schöpfer herstammt, wird nichts in der Welt angetroffen, woraus nicht irgendeine Maximum- oder Minimumeigenschaft hervorleuchtet.” |
| Leonhard Euler (1707 - 1783) |
Kurzreferat: Die Behandlung der Extremwertaufgaben in den aktuellen Schulbüchern weist gewisse Mängel auf. Der größte Teill der Extremwertaufgaben ist von geometrischer Art. Die Methoden der Dynamischen Geometrie eröffnen neue Möglichkeiten der präformalen Behandlung geometrischer Extremwertaufgaben: Durch direkte Manipulation beweglich gemachte Figuren gestatten eine experimentelle Untersuchung quantitativer Figureneigenschaften mit dem Ziel, extremale Eigenschaften zu entdecken und approximativ zu bestimmen. Ein wesentliches Mittel ist dabei die Veranschaulichung quasi empirischer Funktionen in Form von Schaubildern. Als adäquates Werkzeug wird Cabri Géomètre II verwendet.
1. Einleitung
Das Optimieren, zu dem auch das Lösen von Extremwertaufgaben gehört, ist eine der fundamentalen Ideen für den Mathematikunterricht (vgl. u.a. Schupp 1997). Der motivationale Bezug ist klar: Unsere Lebensgestaltung kann als ein permanenter Optimierungsprozess aufgefaßt werden.
Leider ist z.B. die lineare Optimierung im IR2 bzw. IR3 mit einem gewissen lebenspraktischen Bezug nicht mehr verbindlicher Unterrichtsgegenstand in der Sekundarstufe I bzw. II; sie ist wie manch anderer Unterrichtsgegenstand den kostensparenden Stundentafelkürzungen zum Opfer gefallen. Auch wird die Klasse der schönen und anwendungsträchtigen isoperimetrischen Probleme im Mathematik-unterricht nicht thematisiert. Für echte Anwendungsprobleme, wie sie in der Variationsrechnung oder im Operations Research behandelt werden, fehlen das mathematische Werkzeug – und die Unterrichtszeit.
Einen unterhaltsamen Überblick über die inhaltliche und methodische Vielfalt der Maxima- und Minima-Aufgaben geben die "klassischen" didaktischen Arbeiten von Rademacher/Toeplitz (1930), Pólya (1962) und Courant/Robbins (1962); neuere didaktische Monographien über elementare Behandlungen von Extremwertaufgaben stammen von Quaisser/ Sprengel (1986), Claus (1992) und Schupp (1992). Ärmlich wirkt gegenüber dem Inhalt solcher Arbeiten das Repertoire an Extremwertaufgaben, die mit Differentialrechnung der Funktionen einer reellen Variablen gelöst werden können und die sich im Laufe nahezu eines Jahrhunderts, seit der zögerlichen Einführung der Infinitesimalrechnung an Gymnasien im Gefolge der "Meraner Vorschläge" (1905), angesammelt haben.
Neben den sogenannten Funktionsbestimmungsaufgaben dienen die Extrem-wertaufgaben der Anwendung der Kurvendiskussion im Rahmen eines "aufgabenstellenden" Mathematikunterrichts. Dabei lassen die aktuellen lehrplankonformen Schulbücher der gymnasialen Oberstufe im allgemeinen folgende Mängel bei den Aufgabenstellungen erkennen: Die Mittel zur Veranschaulichung von Aufgabenstellungen sind beschränkt; es gibt nur geschlossene Aufgaben und nur lösbare Aufgaben (keine Problematisierung der Existenz einer Lösung!); Aufgabenagglomeration (keine strukturierende Aufgabensequenzierungen); frag-würdige Einkleidungen (sog. "Plantagenaufgaben"); zu wenig Aufgaben, die sich für eine (grobe) mathematische Modellierung eignen; die Minima-Aufgaben sind unterrepräsentiert; Vernachlässigung der heuristischen Dimension (Aufgaben mittels Analogisieren, Generalisieren etc. generieren!); es fehlen Aufgaben, die die Grenzen des Lösens mittels der schulüblichen Differenzialrechnung aufweisen.
Das Lösen der Extremwertaufgaben ist gekennzeichnet durch einen Lösungsschematismus, ohne Reflektion der Methodenangemessenheit und des Inbeziehungsetzens zu anderen Lösungsmethoden. (Wenigstens angedeutet ist das in der "Infinitesimalrechnung" von Keil et al. 1991; als vorbildlich zu nennen ist in dieser Hinsicht das leider nicht mehr vertriebene Schulbuch von Danckwaerts et al. 1991.) So wird z.B. auch auf quadratische Ziefunktionen das entsprechende Lösungsschema angewendet - ganz abgesehen von den zahlreichen Aufgaben die elementar mittels der Ungleichung vom arithmetischen und geometrischen Mittel lösbar sind.
Letztlich sind die hier aufgelisteten Mängel die Folge eines tradierten Curriculums, in dem der Lehrer/die Lehrerin, unter Zeit- und Stoffdruck stehend, gute Prüfungs- ergebnisse mit seiner/ihrer Klasse im Abitur erzielen muß, um als "guter" Lehrer/"gute" Lehrerin anerkannt zu werden. - Die Frage nach der mathematischen Bildung wird längst nicht mehr gestellt! Diesbezügliche Vorschläge für eine Verbesserung der mathematischen Aufgabenkultur beinhaltet z.B. die Methode des Open-ended Approach (Becker/Shimada, 1997).
Ein weiteres Manko des Analysisunterrichts ist die fehlende Integration von Computeralgebrasystemen als Komponenten mathematischer Assistenzprogramme wie z.B. Derive, Mathematica (mittels dem sich auch Extremwertaufgaben mit Nebenbedingungen automatisch lösen lassen!). Ein erstes ansprechendes Integrationskonzept unter Verwendung von Derive, in dem die oben genannten Mängel bei der Behandlung von Extremwertaufgaben weitgehend beseitigt sind, hat Baumann (1998) in seinem projektorientierten Unterrichtswerk vorgelegt. - Ob es nun bald ein Abitur gibt, bei dem Mathematikaufgaben mit Computeralgebra gelöst werden können und sollen? Oder hat der Autor für sein perspektives Werk nur einen mutigen Verlag gefunden und das Interesse von ein paar Computerfreaks in der Lehrerschaft?
2. Die dynamische Behandlungsmethode
Wir gehen nun auf die Nutzung der dynamischen Computergrafik zur Behandlung von geometrischen Extremwertaufgaben ein:
Die geometrischen Extremwertaufgaben oder die Extremwertaufgaben, die sich geometrisch modellieren lassen, bilden den größten Teil des Repertoires an Extremwertaufgaben. Sie setzen die Beherrschung der planimetrischen und stereometrischen Berechnungsaufgaben der Sekundarstufe I voraus. Im Sinne des Spiralcurriculums bilden die geometrischen Extremwertaufgaen der Sekundarstufe II eine Fortsetzung dieser Berechnungsaufgaben.
In einer traditionellen Lernumgebung sind die geometrischen Figuren bzw. ihre zeichnerische Repräsentanz, auf die sich die Berechnungsaufgaben beziehen, starr; sie können durch Bildersequenzen nur unzureichend vor dem "geistigen Auge" beweglich gemacht werden (wenn wir einmal vom flüchtigen Eindruck eines entsprechenden fremdgesteuerten Unterrichtsfilms, der meist nur einen Satz geometrischer Daten visualisieren kann, absehen).
Peter Treutlein, Direktor des Karlsruher Goethe-Realgymnasiums, hat schon 1911 die Forderung nach der Figurenbeweglichkeit folgendermaßen formuliert:
"Als einer der Hauptunterschiede altgriechischer und neuzeitlicher Geometrie gilt das, daß in jener die Figuren sämtlich als starr und fest gegeben angenommen werden, in dieser als beweglich und gewissermaßen fließend, in stetem Übergang von einer Gestaltung zu anderen begriffen. Sollen unsere Schüler in die heutige Form der Wissenschaft und gar gelegentlich in deren Anwendung eingeführt werden, so müssen sie beizeiten daran gewöhnt werden, die Figuren als jeden Augenblick veränderlich zu denken und dabei auf die gegenseitige Abhängigkeit ihrer Stücke zu achten, diese zu erfassen und beweisen zu können.
Der Auffassung der Figuren als starrer Gebilde kann und muß in verschiedener Weise entgegen gearbeitet werde.
Das eine hierzu Erforderliche ist das Beweglichmachen der Teile einer Figur..."
Das Verstehen von geometrischen Extremwertaufgaben setzt u. E. individuelle Erfahrungen mit beweglichen Figuren voraus. Diese Erfahrungen können heute an Bildschirmfiguren, die mittels direkter Manipulation "kontinuierlich" variierbar sind, gesammelt werden.
Die direkte Manipulation geometrischer Konfigurationen ist das wesentliche Kennzeichen der sogenannten dynamischen Geometrie oder Zug-Modus-Geometrie, vgl. u.a. Schumann (1992) - Zur Erzeugung solcher Bildschirmkonfigurationen verwenden wir Computerwerkzeuge für die planare Schulgeometrie, wie das geometrieinhaltlich und software-ergonomisch vorbildliche Cabri-Géomètre II (Laborde 1996).
Mit CABRI II steht eine neue Methode der Untersuchung von funktionalen Eigenschaften einer geometrischen Figur zur Verfügung: Wir können Messungen an den konstruierten geometrischen Figuren vornehmen, aus den Meßwerten mathematische Ausdrücke bilden, die funktionalen Eigenschaften (z.B. Beziehungen zwischen Längen, Flächeninhalte, Winkelbeziehungen,...) quantitativ beschreiben; für gewisse Standardterme lassen sich auch entsprechende Berechnungsmakros definieren. Durch Verziehen der Figur im Zug-Modus verändern wir den Meßwert oder den Wert des gebildeten Terms, der beim Vorgang der Figurenvariation beobachtet und untersucht werden soll. Eine funktionale Eigenschaft kann zusätzlich in einer Wertetabelle oder, im Falle einer nur von einem Parameter abhängigen Eigenschaft, als Schaubild einer empirischen Funktion dargestellt werden.
Aus dieser Möglichkeit, funktionale Eigenschaften einer Figur zu untersuchen, ergibt sich folgende Methode zur Entdeckung von extremalen Eigenschaften und zur näherungsweisen Bestimmung von Extremwerten:
| (1) | Konstruktion einer geometrischen Figur, die auch Nebenbedingungen erfüllt. |
| (2) | Variation einer unabhängigen Größe der Figur bwz. Teilfigur unter Beobachtung eines funktionalen Zusammenhangs: unabhängige Größe - abhängige Größen (Datensammlung in Werte-Tabelle; grafische Darstellung im Schaubild) |
| (3) | Erkennen einer extremalen Eigenschaft (näherungsweise Bestimmen von Extremstelle und Extremwert) |
| (4) | Variation der Figurenparameter und Prüfung, ob extremale Eigenschaft invariant |
| (5) | Formulierung einer allgemeinen geometrischen Extremwertaufgabe |
Jetzt erst schließt sich die exakte Lösung der allgemeinen Extremwertaufgabe mittels Differentialrechnung (z.B. unter Einsatz von Computeralgebra) oder mittels elementarer Methoden an. -Diese Methode ist präformal, da sie im allgemeinen nicht das Aufstellen einer Zielfunktion notwendig macht, aber trotzdem gestattet, die Zielfunktion als eine quasi empirische Funktion auf extremale Eigenschaften hin zu untersuchen. Damit ist diese Methode auch relevant für die Sekundarstufe I.
Da wir allenfalls davon ausgehen können, daß die Schüler und Schülerinnen Novizen in der Nutzung eines geometrischen Computerwerkzeugs sind, stellen wir die Bildschirm-Konfiguration zusammen mit den Aufgabentexten als "interaktive Arbeitsblätter" (Schumann 1998), die auch zu Demonstrationszwecken verwendet werden können, zur Verfügung. Der Einsatz solcher Arbeitsblätter bietet einen ersten Zugang zur dynamischen Behandlung von geometrischen Extremwertaufgaben.
3. Beispiele für die dynamische Behandlung
Im folgenden illustrieren wir die Methode der dynamischen Behandlung geometrischer Extremwertaufgaben an einigen Beispielen:
Eine Vorbemerkung: Die printmediale Wiedergabe einer dynamischen Darstellung beansprucht jene Vorstellungskraft, die gerade durch den Einsatz von dynamischen Computergrafik gefördert werden soll. Insofern sind Printmedien zur Erklärung dynamischer Bildschirmvorgänge ungeeignet; angemessen wäre ein Internet-Dokument, das dem Leser gestattet, in den Abbildungen direkt manipulativ tätig zu werden. Noch besser wäre natürlich ein im Internet verfügbares "interaktives Schulbuch".
Am Beispiel 1 erläutern wir näher die wesentlichen Möglichkeiten der dynamischen Behandlung, die in anderen Beispielen nur wahlweise angewendet werden.
Beispiel 1 (Eine Zaunaufgabe)

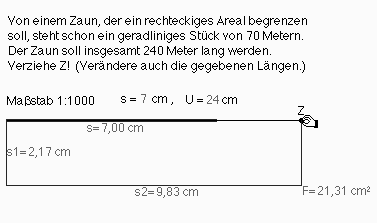
Die Abbildung 1a zeigt die offene Aufgabenstellung. Durch Verziehen von Z (symbolisiert durch die greifende Hand) verändert sich die Form des "Zaunrechtecks", dessen Umfang sich nicht ändert, wohl aber die anderen Daten (Abb. 1b); auch die Grenzlage für s1=0 cm kann realisiert werden (für die Messung des Flächeninhaltes steht ein Werkzeug zur Verfügung). Bereits hier kann der Nutzer des interaktiven Arbeitsblattes feststellen, daß der Flächeninhalt streng monoton von s2=s nach s2=U/2 abnimmt und daß das Flächenmaximum 3500m2 bei den Abmessungen 50m auf 70mangenommen wird. Die Flüchtigkeit der einzelnen Zustände erschwert eine überblickende Bewertung der entsprechenden Daten. Deswegen können diese in eine Tabelle eingetragen werden (Abb. 2). Hier könnten wir noch die Spalte s2 - s1 anfügen, die zeigt, wie der Flächeninhalt bei abnehmender Differenz zunimmt.
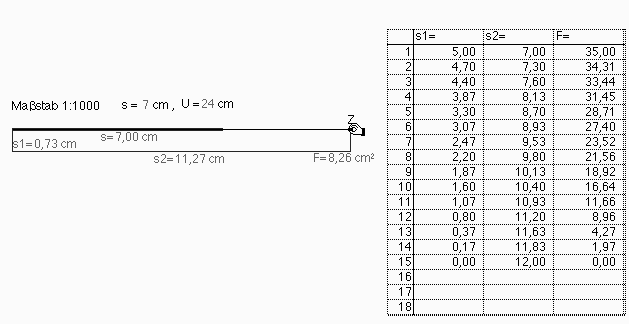
Abb. 2
Zur grafischen Veranschaulichung der funktionalen Abhängigkeit s1 ® F(s1) bei festem U und s werden s1 und F auf der s1-Achse und F-Achse abgetragen. Der Punkt (s1; F) erzeugt das Schaubild als Spur (Abb. 3), die für Untersuchungen bei Variation der Parameter s und U durch ein grafisches Objekt ersetzt wird (Abb.4a). Das Randmaximum ist nicht invariant; z.B. für s = 5 (cm) und U = 26 (cm) erhalten wir ein relatives Maximum für den Flächeninhalt, das zugleich absolutes Maximum ist (Abb. 4b). Welches ist die Bedingung für diesen Wechsel?...
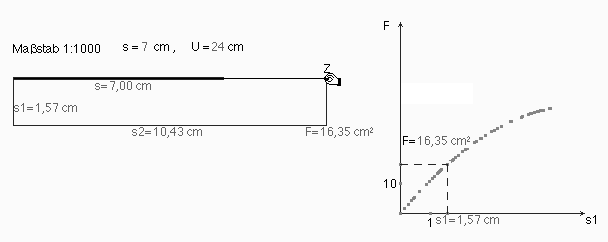
Abb. 3
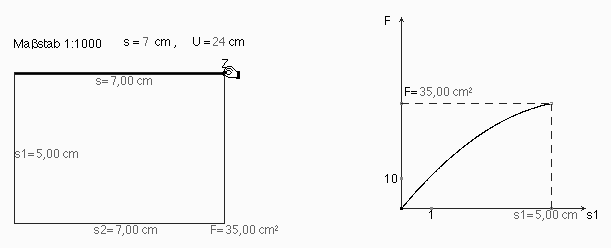
Abb. 4a
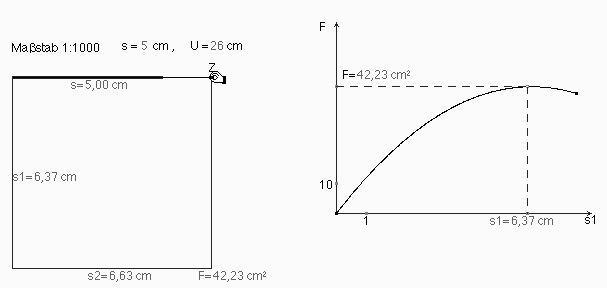
Abb. 4b
Beispiel 2 (Eine Verpackungsaufgabe)
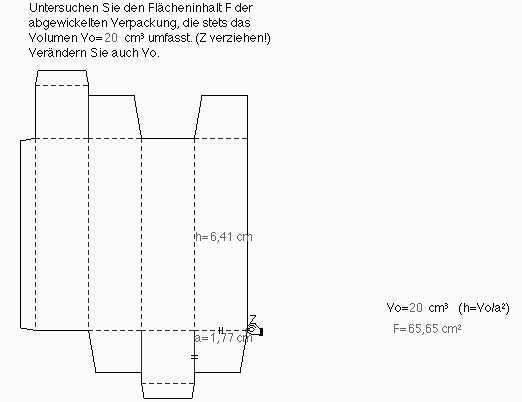
Abb. 5a
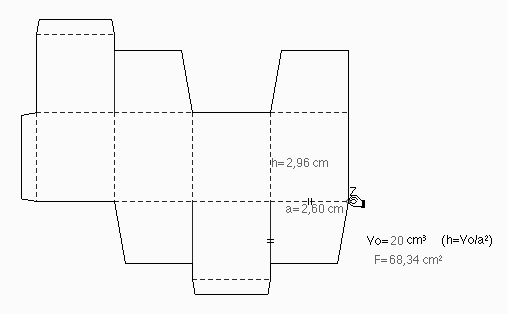
Abb. 5b
Der Flächeninhalt eines real existierenden Typs von Verpackungsnetzen ist zu untersuchen (Abb. 5a). Dabei ist das "verpackte" Volumen invariant. (Solche Netze können auch ausgedruckt, ausgeschnitten und ausgefaltet werden.) Durch Verziehen erzeugen wir unterschiedliche (nicht äquiforme) Verpackungsnetze mit unterschiedlicher Flächenbeanspruchung (Abb.5b). Mittels des Schaubildes bestimmen wir das Flächenminimum näherungsweise (Abb. 6). Die Art des Minimums erweist sich bei Variation des Parameterwertes V0 als invariant.
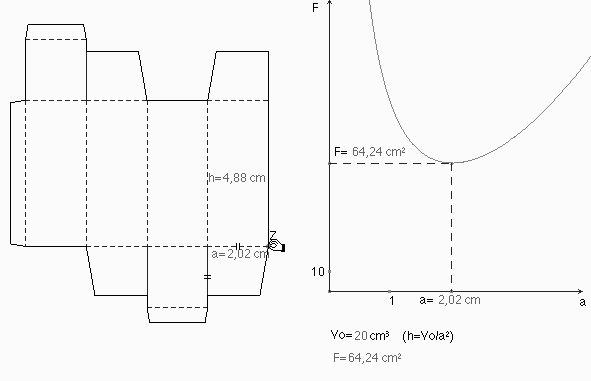
Abb. 6
Beispiel 3 (Eine räumliche Einbeschreibung)
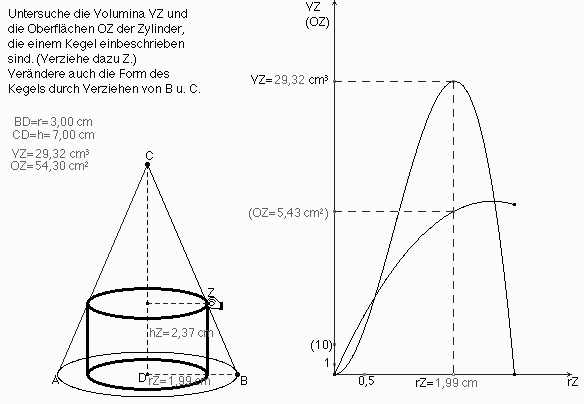
Abb. 7a
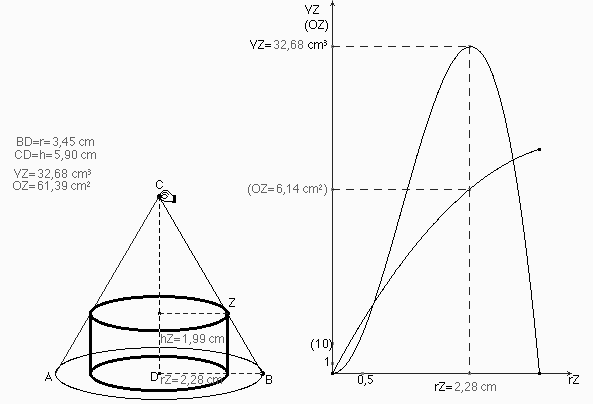
Abb. 7b
Unter den einbeschriebenen Zylindern hat einer maximales Volumen, ein anderer maximale Oberfläche (Abb. 7a). Ist dieses Extremalverhalten invariant bei Änderung der Kegelform? So gibt es beispielsweise für einen Kegel mit r = 3,45 LE und h = 5,90 LE keinen eingeschriebenen Zylinder mit maximaler Oberfläche mehr (Abb. 7b).
Wie lautet die Bedingung für die Existenz eines Oberflächenmaximums?...
Beispiel 4 (Eine Dosenaufgabe)
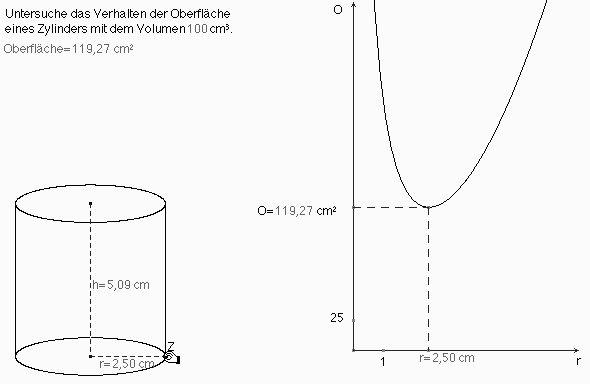
Abb. 8
Unter allen volumengleichen Zylindern gibt es nur einen, der minimale Oberfläche hat. Seine volumenabhängigen Daten können wir näherungsweise ablesen (Abb. 8). Diese Aufgabe dient einer ersten groben Modellierung des Anwendungsproblems unter allen Verpackungsdosen, die mit dem geringsten Materialaufwand zu bestimmen.
Beispiel 5 (Eine Touristenaufgabe)
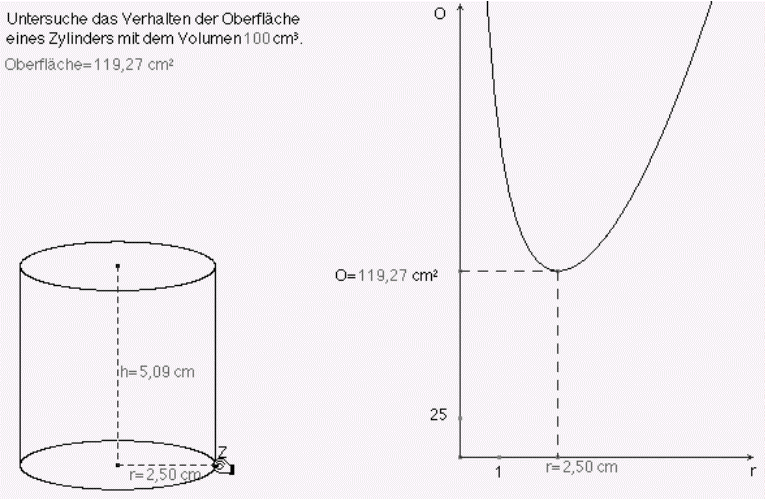
Abb. 9
Bei diesem sehr anschaulichen Problem ist gut zu erkennen, wie der das Standbild erfassende Blickwinkel vom Abstand des Betrachters abhängt und wie der Formtyp des Schaubildes invariant ist bei Variation der Problemparameter.
Beispiel 7 (Aus der Koordinatengeometrie)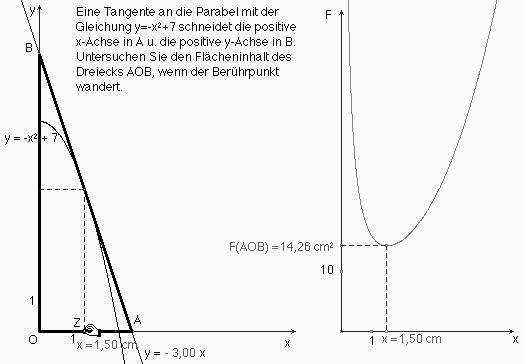
Abb. 10
Auch die üblichen koordinatengeometrischen Extremwertaufgaben können dynamisch behandelt werden!
Beispiel 6 (Eine Quaderaufgabe)
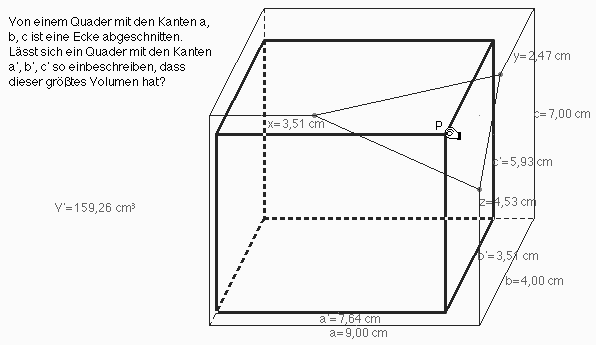
Abb. 11
Dieses Aufgabenbeispiel soll die Grenzen der dynamischen Behandlungsmethode bei der Nutzung von 2-D-Werkzeugen verdeutlichen, die zielgerichtet nur auf Aufgaben anwendbar ist, denen Funktionen einer reellen Variablen zugrunde liegen.
Bei dieser Aufgabe, dem räumlichen Analagon einer ebenen, unserer Behandlungs-methode leicht zugänglichen Aufgabe, ist der Eckpunkt P des einbeschriebenen Quaders so auf der dreieckigen Schnittfläche zu verziehen, daß dieser (näherungsweise) maximales Volumen annimmt, was durch mehr oder minder systematisches Probieren herausgefunden werden kann...
4. Schlußbemerkung
Im Zusammenhang mit der Computernutzung im Mathematikunterricht hat die Mathematikdidaktik u.a. die Aufgabe, Integrationskonzepte, wie z.B. das hier vorgestellte, zu entwickeln und auch systematisch in der Unterrichtspraxis zu evaluieren.
Aus lernpsychologischer Sicht induziert die Integration von Computerwerkzeugen in den Mathematikunterricht durch betreffendes instrumentelles Wissen eine Veränderung aller bei einem mathematischen Lernprozeß intervenierenden Arten des Wissens (vgl. Diagramm). -Wir wissen heute noch fast nichts über solche Veränderungen.
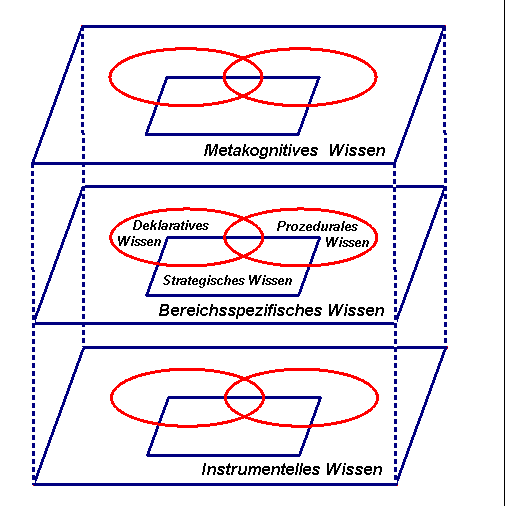
Diagramm (Arten des Wissens bei der Nutzung von Computerwerkzeugen)
5. Literatur
|
Arbinger, R. (1997): |
Psychologie des Problemlösens. Eine anwendungsorientierte Einführung. - Darmstadt: Primus |
|
Baierlein, M. et al. (1997): |
Anschauliche Analysis 1. - München: Oldenburg |
|
Baumann, R. (1998): |
Analysis 1, Grenzwerte, Differenzialrechnung, Optimierungsaufgaben. Ein Arbeitsbuch mit Derive. - Stuttgart: Klett. |
|
Becker, J. B. u. S. Shimada (1997): |
The Open-Ended Approach. A New Proposal for Teaching Mahtematics. - Reston, VA: NCTM |
|
Bigalke, A.; N. Köhler (1995): |
Analysis, Kursstufe. - Berlin: Cornelsen |
|
Blum, W.; Törner, G. (1983): |
Didaktik der Analysis. - Göttingen: Vandenhoek und Ruprecht. |
|
Bock, H.; Walsch, W. (1993): |
Mathematik entdecken, verstehen, anwenden. Analysis. - München: Oldenburg |
|
Bronstein, I. N.; Semendjajew, K.A. (1984): |
Taschenbuch der Mathematik. - 7. Auflage - Frankfurt/M.: Harri Deutsch |
|
Claus, H. J. (1992): |
Extremwertaufgaben. - Darmstadt: Wissenschaftliche Buchgesellschaft |
|
Courant, R.; Robbins, H. (1962): Danckwerts, R. et al. (1991): |
Was ist Mathematik? - Berlin: Springer
Analysis für den Leistungskurs, Klasse12/13. - Stuttgart: Metzler |
|
Griesel, H.; Postel, H. (1992): |
Mathematik heute, Leistungskurs Analysis, Gesamtband. - Hannover: Schroedel/Schöningh |
|
Keil, K. - A. et al. (1991): |
Die Infinitesimalrechnung. - München: Bayerischer Schulbuchverlag |
|
Kuypers, W.; Lauter, J. (1993): |
Mathematik Sekundarstufe II, Analysis Leistungskurs. - Berlin: Cornelsen |
|
Laborde, J.-M.; Bellmain, F. (1996): |
Cabri Géomètre II. Version 1.0 - Dallas/USA u. Freising: Texas Instruments. (Deutsche Oberfläche und Bearbeitung des Handbuchs von H. Schumann) |
|
Locher-Ernst, L. (1948): |
Differential- und Integralrechnung im Hinblick auf ihre Anwendungen. - Basel: Birkhäuser |
|
Pólya, G.( 1962): |
Mathematik und plausibles Schliessen, Band 1: Induktion und Analogie in der Mathematik. - Basel: Birkhäuser |
|
Quaisser, E., Sprengel, H.-J. (1986): |
Extrema. - Berlin: Deutscher Verlag der Wissenschaften |
|
Rudio, F. et. al., Hrsg. (seit 1942): |
Leonhard Euler: Opera omnia. Ser. I. Opera mathematica. - Lausanne: Societas scientiarium naturalium Helvetica |
|
Schmid, A.; Schweizer, W. (1990): |
Analysis Leistungskurs, Gesamtausgabe. - Stuttgart: Klett. |
|
Schmidt, W. (1984): |
Mathematikaufgaben, Anwendungen aus der modernen Technik und Arbeitswelt. - Stuttgart: Klett. |
|
Schumann, H. (1984): |
Inhalts- und umfangsextremale Eigenschaften achsensymmetrischer Vierecke. - In: MU (30), Heft 6, S. 38 - 44. |
|
Schumann, H. (1991): |
Experimentelles Lösen einfacher isoperimetrischer Probleme in einer interaktiven computergrafischen Lernumgebung. - In: Didaktik der Mathematik (19), Heft 3, S. 227 - 241 |
|
Schumann, H. (1992): |
Schulgeometrisches Konstruieren mit dem Computer. - Stuttgart: Metzler u. Teubner |
|
Schumann, H. (1993): |
Eine Folge von Verpackungsproblemen. - In: MNU (36), Heft 1, S. 7 - 14 |
|
Schumann, H. (1997): |
Neue Standards für das Lösen geometrischer Berechnungsaufgaben durch Computernutzung. - In: MNU (50), Heft 3, S. 172 - 175 |
|
Schumann, H. (1998): |
Dynamische Behandlung elementarer Funktionen - In: Mathematik in der Schule (36), Heft 3, S. 172 - 188. |
|
Schumann, H. (1998): |
Interaktive Arbeitsblätter für das Geometrielernen. - In: Mathematik in der Schule (36), Heft 10, S. 562 - 569 |
|
Schumann, H.; Green,D. (1994): |
Discovering Geometry with a Computer. - Bromley/Kent: Chartwell-Bratt |
|
Schupp, H. (1992): |
Optimieren - Extremwertbestimmung im Mathematikunterricht. - Mannheim: B.I. Wissenschaftsverlag. |
|
Schupp, H. (1997): |
Optimieren ist fundamental. - In: mathematik lehren 81 (April 1997), S. 4 - 10 |
|
Tietze, U.-P.; Klika, M.; Wolpers, H.(1997): |
Mathematikunterricht in der Sekundarstufe II, Band 1: Fachdidaktische Grundfragen - Didaktik der Analysis. - Braunschweig: Vieweg |
|
Treutlein, P. (1911): |
Der geometrische Anschauungsunterricht. - Leipzig: B.G. Teubner |
|
Winter, H. (1989): |
Entdeckendes Lernen im Mathematikunterricht. - Braunschweig: Vieweg |
|
Wittmann, E. (1981): |
Grundfragen des Mathematikunterrichts - 6. Auflage - Braunschweig: Vieweg |
|
Wolff, G. (1962): |
Die Elemente der Mathematik, Band 3 Arithmetik, Algebra und Analysis - 7. Auflage - Paderborn: Schöningh, Hannover: Schroedel |
|
Wolfram, S. (1991): |
Mathematica. A System for Doing Mathematics by Computer. - 2nd Edition. - Redwood City, CA: Addison-Wesley |
Adresse des Autors:
Prof.Dr.habil. Heinz Schumann
Fak. III, Mathematik/Informatik
Institut für Bildungsinformatik
PH Weingarten
Kirchplatz 2
D-88250 Weingarten
Email: schumann@ph-weingarten.de