Heinz Schumann
Medienspezifische Methodenvielfalt
bei der Behandlung einer Extremwertaufgabe
| Viele Wege führen zum Ziel. |
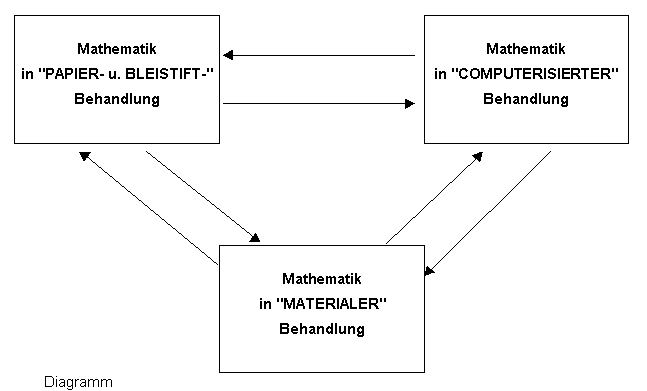
Heute ist zu den zwei traditionellen Behandlungsarten für mathematische Gegenstände eine dritte Behandlungsart, nämlich die computerisierte, hinzugekommen (vgl. Diagramm).
-Folgende offene Fragen im Kontext des Mathematikunterrichts werden induziert: Wie können die drei Behandlungsartenen integriert werden? D.h., wie gestalten sich die Schnittstellen zwischen den einzelnen Behandlungsarten? Welche Vor- und Nachteile bringt die Behandlung eines mathematischen Gegenstandes mittels einer der Behandlungsarten mit sich?
Wir charakterisieren hier nur grob die medienspezifischen Behandlungsarten:
"Materiale" Behandlung eines mathematischen Gegenstandes: "Materiales" Konstruieren, wie Schneiden, Reißen, Falten, Zusammenbauen, Zerlegen, …; Ausmessen materialer Objekte, …(ein wesentliches Merkmal: ganzheitlich-sensorische Wahrnehmung)
"Papier- u. Bleistift"-Behandlung: Numerisches, algebraisches und geometrisches Konstruieren, wie Rechnen, Termumformen, Gleichungslösen, Konstruieren mit Zirkel, Lineal und Geo-Dreieck, …(ein wesentliches Merkmal: Algorithmische Fertigkeiten)
"Computerisierte" Behandlung:
Am Beispiel der folgenden geometrischen Extremwertaufgabe versuchen wir, das Zusammenspiel der verschiedenen medienspezifischen Behandlungsarten im Rahmen des Mathematikunterrichts der Sekundarstufe I exemplarisch zu verdeutlichen.
Extremwertaufgabe: Untersuche das Volumen eines Kegels, von dem nur die Mantellinie gegeben ist, daraufhin, ob es ein Maximum hat. Oder: Welchen Mittelpunktswinkel muss ein Kreissektor mit festem Radius besitzen, damit dieser zum Mantel eines Kegels von größtem Rauminhalt aufgeformt werden kann?
Wir geben für diese Aufgabe im folgenden verschiedenen Behandlungsmöglichkeiten an, die im Schlussteil dieser Arbeit diskutiert werden sollen. Erst durch die Nutzung von Computerwerkzeugen eröffnet sich eine entsprechende Methodenvielfalt. (Die Auswahl der benutzten Comuterwerkzeuge orientiert sich an den subjektiven Erfahrungen des Autors.)
Die elementaren Behandlungsmethoden richten sich nach den mathematischen Werkzeugen, die von der Klassenstufe 9 an (Satz des Pythagoras!) zur Verfügung stehen.
2. Eine mehrmethodische Behandlung der Extremwertaufgabe
Wir beginnen mit drei vor allem experimentellen Behandlungen der speziellen Extremwertaufgabe und schließen mit zwei Lösungsmöglichkeiten für die allgemeine Aufgabe.
2.1 "Vom Papiermodell zur Tabellenkalkulation"
Aufgabe:
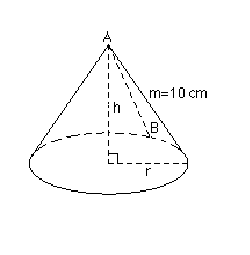
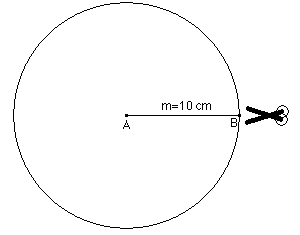
a) Zeichne einen Kreis vom Radius 10 cm. Schneide diesen aus und längs einer Radiusstrecke AB auf (Abb. 1a). Forme aus der Kreisscheibe einen Kegelmantel mit A als Kegelspitze, in- dem du B entlang der Kreislinie verschiebst (Abb.1 b; verwende eine Büroklammer, um die Überlappung zu fixieren).
b) Miss den jeweiligen Durchmesser der Kegelstandfläche für verschiedene Kegelmäntel mit der Mantellinie m=10 cm, indem du die aufgeformten Mäntel auf ein Lineal stellst. Miss auch
 |
 |
|
|
|
die Höhe des jeweiligen Kegels (am besten spannst du den Kegel waagerecht zwischen zwei Buchstützen). Berechne aus dem jeweiligen Radius r und der zugehörigen Kegelhöhe h das jeweilige Kegelvolumen. Verwende den Taschenrechner; lege eine Tabelle für die Messwerte und den berechneten Wert an. -Kannst du über die Volumina der verschiedenen Kegel eine Vermutung aussprechen? (Denk z.B. daran, welche Fülleigenschaft ein kegelförmiger Filter oder ein kegelförmiges Sektglas haben soll.)
c) Verwende nun ein Tabellenkalkulationsprogramm (z.B. EXCEL oder das von WORKS). Lege eine dreispaltige Tabelle mit einer Kopfzeile für den Radius r (cm), die Höhe h (cm) und das Volumen V (cm³) an. Gib davon in die erste Spalte die Radien von 0 bis 10 (cm) ein mit einer Schrittweite von 1; dann in die erste Zeile der zweiten und dritten Spalte die Formeln für die Höhe h und das Volumen V ein und kopiere die Formeln nach unten.
Zwischen welchen ganzzahligen Radien vermutest du das größte Volumen?
Verfeinere die Schrittweite zu 0,5 usw. bis du erkennst, für welchen Radius (auf zwei Stellen nach dem Komma) das Kegelvolumen den größten Wert annimmt. Danach kannst du auch für eine andere Mantellinie (z.B. m=15 cm) das größte Volumen auf gleiche Art und Weise bestimmen.
2.2 Mit Hilfe eines Funktionsplot-Programms
Aus V = 
folgt mit h2 = m2 - r2
V = 
und für m = 10(cm)
V = 
.
Mittels des Funktionsplotters von DERIVE lässt man für V in Abhängigkeit von r ein Schaubild erstellen (Abb. 2). Wir fahren mit dem Grafikcursor (+) auf den maximalen Punkt im Schaubild und lesen die Koordinaten der Cursorposition ab. Damit gewinnen wir einen Nährungswert von Augenmaßqualität für die Maximalstelle und Maximalwert. Variation der Länge
der Mantellinie führt auf entsprechende Nährungslösungen.
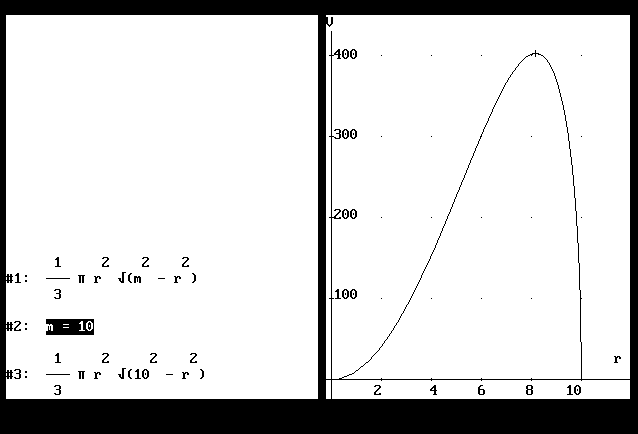
Abb. 2
2.3 Durch direkte Manipulation auf einem interaktiven Arbeitsblatt
Das interaktive Arbeitsblatt (Abb. 3 a) ist in Cabri Géomètre II, einem vorbildhaften dynamischen Geometriesystem, kreiert worden; auf dem Arbeitsblatt können verschiedene Zusatzwerkzeuge, z.B. eine Tabelle mit entsprechender Kopfzeile, ein Koordinatensystem (1. Quadrant) mit entsprechend laufendem Punkt, eingeschaltet werden.
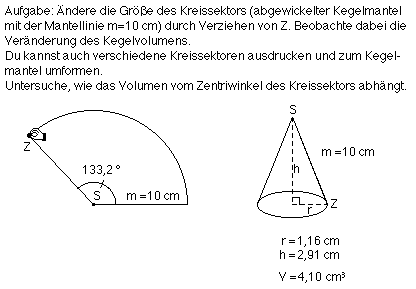
Abb. 3 a
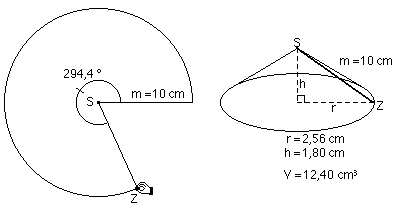
Abb. 3 b
Die Abbildung 3 b zeigt bereits eine Nährungslösung. Die verschiedene Daten können zur besseren Übersicht in eine Tabelle beim Verändern des Mittelpunktwinkels eingetragen werden (Abb. 4). Das Schaubild veranschaulicht die Abhängigkeit des Volumens von der Größe des Zentriwinkels; ihm kann ebenfalls per Augenmaß eine Nährungslösung entnommen werden (Abb. 5). Bei Veränderung der Mantelliniengröße erkennt man, dass der Mittelpunktswinkel für das Volumenmaximum invariant ist. (Abb. 6)
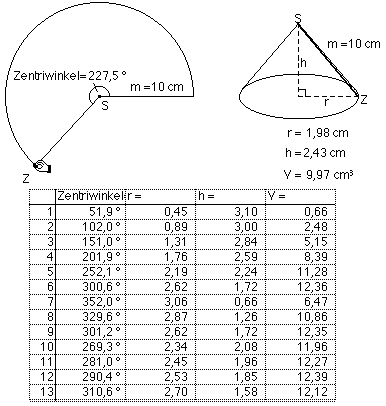
Abb. 4
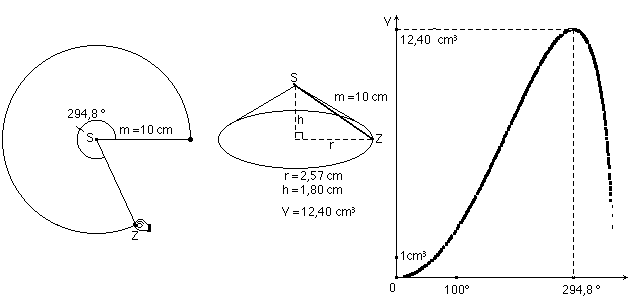
Abb. 5
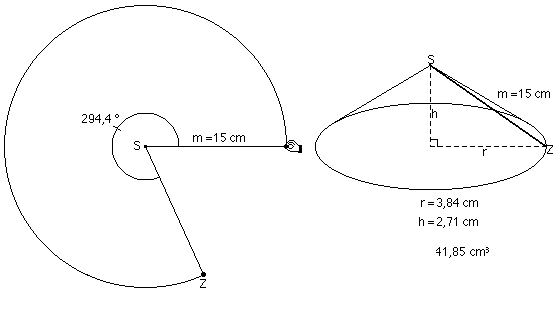
Abb. 6
2.4 Mit einer Computernumerik-Black-Box
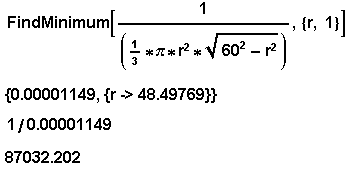
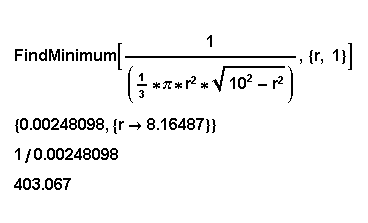Im mathematischen Assistenzprogramm MATHEMATICA steht für das Lösen von speziellen Extremwertaufgaben für Funktionen einer reellen Variablen das Kommando "Find Minimum" zur Verfügung, das z.B. für alle x ³
x0 die absoluten Minimalstellen mit ihrem Funktionswert berechnet. Da wir das Maximum für 
suchen, verwenden wir einfach den reziproken Ausdruck und erhalten für r ³
1 die im Ausdruck 1 a ausgegebene Lösung; für das Zuckertütenmaß m = 60 (cm) ergibt sich eine etwas außergewöhnliche volumenmaximale Tüte für Schulanfänger (Ausdruck 1 b).
Ausdruck1 a Ausdruck 1 b
2.3 Mittels "händischer Algebra"
Aus V= 
ergibt sich durch Quadrieren das ganzrationale
V2 = (
p
)2 ×
r4 (m2-r2). Für m=10 erkennen wir, dass r ®
V2 an derselben Stelle wie r ®
V ihr Maximum hat (Abb. 7 a/b). Wir können also die maximale Stelle für r ®
V bestimmen, indem wir sie für r ®
V² berechnen.
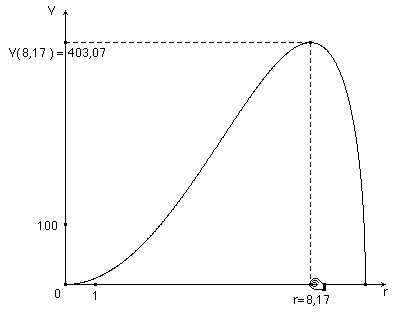
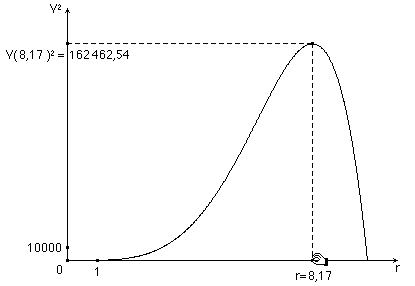
Abb. 7 a/b
Es wird so umgeformt, dass sich rechts ein Produkt mit konstanter Faktorensumme ergibt. (Hier machen wir uns zu Nutze, dass ein Produkt aus drei Faktoren, dessen Faktorensumme konstant ist, maximal wird, genau dann, wenn die Faktoren einander gleich sind.- Das kann leicht experimentell mit dem Taschenrechner überprüft werden.)
, wobei 
(konstant).
Das Produkt 
wird am größten für 
, also für 
, daraus folgt 
und 
(für m=10 cm: rmax »
8,16 cm, hmax »
5,77 cm) und das Verhältnis von rmax zu hmax ist gleich 
zu 1, d.h. rmax und hmax stehen im gleichen Verhältnis wie Länge und Breite einer DIN A4 Seite (Abb. 8; Achsschnitt des volumenmaximalen Kegels). Für das maximale Volumen erhält man
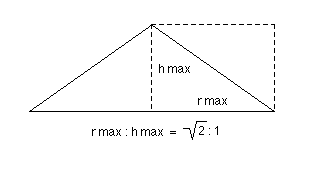Vmax = 
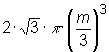(für m=10: Vmax »
403,07 cm³ ).
Abb. 8
Der Mittelpunktswinkel des abgewickelten Kegelmantels wird aus
berechnet: 
(Der Komplementwinkel zu a
max ist somit ca. 66°; es muss also aus einer Kreisscheibe unabhängig von der Radiusgröße ein Sektor mit diesem Winkel herausgeschnitten werden, um den optimalen Kugelmantel zu erhalten.)
2.4 Mit Unterstützung durch Computeralgebra
Wir wenden auf r ® V(r)2 eine Differenzmethode zur Bestimmung der maximalen Stelle an: In der Grenzlage geht die horizontale Sekante in die Tangente durch den Extremalpunkt über (Abb. 9 ). Wegen V(r-d)2=V2(r-d)2 ist V(r+d)2-V(r-d)2=0; diese Differenzgleichung kann in eine wesentliche Gleichung überführt werden, in der wir nach Ersetzung von d durch 0 (Grenzübergang! Abb. 10 a/b) eine Bestimmungsgleichung für rmax erhalten. Zur Einsparung von Umformungs- und Lösungsarbeit verwenden wir die Computeralgebra-Komponente von DERIVE. Den Lösungsweg dokumentiert ein entsprechender Ausdruck (Ausdruck 2).
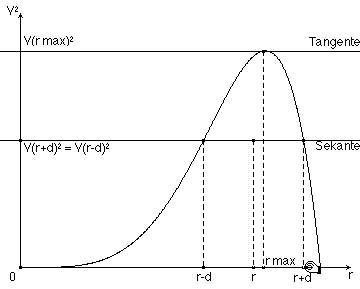Abb. 9
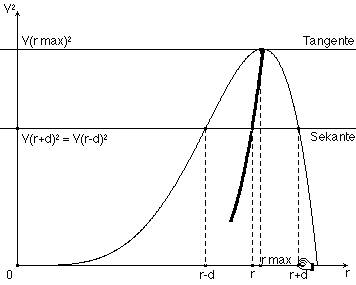
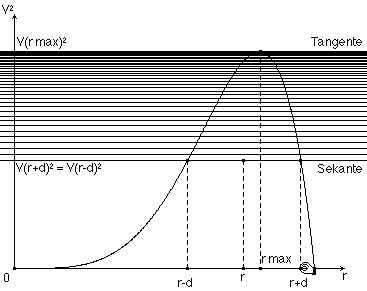Abb. 10 a/b
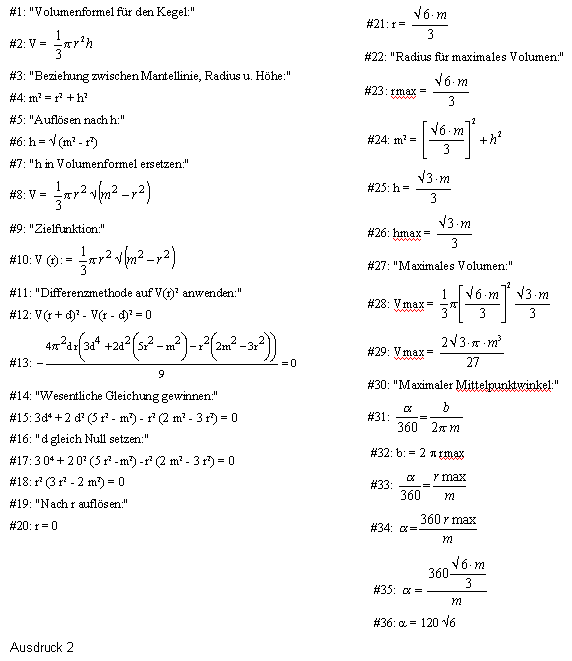
3 Eine Diskussion der Behandlungsmethoden
Die erste Behandlung "Vom Papiermodell zur Tabellenkalkulation" (2.1) geht von der materialen Konstruktion des abgewickelten Kegelmantels und dessen variabler Dimensionierung bei konstanter Größe der Mantellinie aus; es schließt sich das Ausmessen des jeweiligen Kegels (Durchmesser, Höhe) an, um dann mittels Volumenformel und Taschenrechner ein Volumenoptimum zu bestimmen (dabei sind die Daten zur Auswertung in einer Tabelle zu erfassen). Mit dieser Methode kann die Aufgabe schon auf einer niedrigen Klassenstufe als der neunten behandelt werden, wenn die Kegelvolumenformel einfach der Formelsammlung entnommen wird (p ist ja näherungsweise imTaschenrechner verfügbar!). Diese Lösungsmethode ist sehr zeitaufwendig und ungenau (wegen der Gewinnung der zu messenden Daten), aber sie fördert die Raumvorstellung und das Verständnis für die Aufgabe (etwa für die Grenzen bei der Variation des Radius). Die nachfolgende Behandlung mittels einer Tabellenkalkulation setzt unter anderem den Pythagorassatz (Klasse 9) voraus und nicht unerhebliche Kompetenz in der Nutzung eines solchen Computerwerkzeugs, das allerdings nicht nur für mathematikspezifische Aufgaben eingesetzt werden kann. Diese Behandlung wird motiviert durch die Schwächen der vorausgegangenen. Von Vorteil ist die ökonomische Reproduktion von Ergebnissen für andere Mantellinienlängen. Die in einer Tabellenkalkulation leicht generierbareVisualisierung der Daten (Radius, Volumen) durch ein Liniendiagramm ist eher als problematisch anzusehen.
Der Einsatz eines Funktionsplot-Programms (2.2) liefert durch Ansteuern des extremalen Punkts nur Näherungswerte für Extremstelle und –wert. Diese Methode ist aber deshalb von Vorteil, weil sie die funktionale Abhängigkeit des Volumens vom Radius bzw. Mittelpunktswinkels verbildlicht. Allerdings sind dazu gewisse Werkzeugkompetenzen zur Erzeugung des Schaubildes notwendig (etwa in DERIVE: Beherrschung des Editors zur Termeingabe, der Dimensionierung des Koordinatensystems einschließlich der Achsenbenennung.) – Zur Erzeugung einer Kurvenschar r ®
p
r2 
für den Parameter m, z.B. für m von 1 bis 15 mit der Schrittweite 1, eignet sich DERIVE in der Sekundarstufe wegen des kryptischen Kommandos VECTOR (
p
r2 Ö
(m²-r2), m, 1, 15,1) nicht; dafür sind andere Funktionsplotter mit einer geeigneten Kurvenschar-Option vorzuziehen.
Das computerisierte Lernarrangement "Interaktives Arbeitsblatt" (2.3) bietet mit seinen Erweiterungen bei geringer Kompetenz in der Werkzeugnutzung und durch die Möglichkeit der direkten Manipulation eine motivierende, effiziente und zeitökonomische Plattform für die Lösung einer der speziellen Extremwertaufgaben. Die Schnittstelle zur materialen Darstellung ist durch den Ausdruck von Kreissektoren (abgewickelter Kegelmantel) gegeben. Besonders hervorzuheben ist die direkt manipulative Variation der Größe der Mantellinie die zum Erkennen der Invarianz des Mittelpunktwinkels für das maximale Kegelvolumen führt. Der Nachteil dieser Behandlungsmethode besteht darin, dass die betreffende Volumenformel und die entsprechende Anwendung des Pythagoras-Satzes unter der Oberfläche des Arbeitsblattes "versteckt" worden sind. Das kann aber durch die Fragestellung: Wie ist das Arbeitsblatt gemacht? aufgedeckt worden.
Die automatische Computer-Numerik Lösung (2.4) kann allenfalls demonstriert werden, denn das kommandogetriebene MATHEMATICA ist für einen derartigen lokalen und interaktiven Einsatz im Rahmen des Mathematikunterrichts der Sekundarstufe I wenig geeignet. (Der unter der Oberfläche verborgene Optimierungsalgorithmus könnte in der Sekundarstufe II analysiert werden.) Immerhin erfahren die Schüler die numerische Leistungsfähigkeit eines solchen Systems. Trotzdem muss aber der Funktionsterm durch Reziprokbildung dem "FindMinimum" angepasst werden, will man nicht eine Kommando "FindMaximum" programmtechnisch definieren.
Alle vorstehenden Lösungen sind Lösungen für eine der speziellen Extremwertaufgaben. Uns interessiert die Lösung der allgemeinen Extremwertaufgabe, weil nur sie formelhaft alle speziellen Lösungen erfasst und gestattet, eventuell notwendige Determinationen vorzunehmen und besondere Beziehungen zwischen den die optimale Form bestimmenden Größen zu erkennen. Der Übergang zu Lösungsmethoden für die allgemeine Extremwertaufgabe ist also unerlässlich. Es müssen aber solche Lösungsmethoden angewendet werden, die in den Rahmen des Mathematikunterrichts passen, die also ohne die übliche Differentialrechnungsmethode auskommen:
Die händische Lösung (2.5) verwendet den Satz: Unter allen Produkten, deren Faktorsummen konstant sind, hat das Produkt mit einander gleichen Faktoren maximalen Wert. Dieser Satz kann in der Sekundarstufe I schon aus Zeitgründen nur plausibel gemacht werden. Die Erkenntnis, dass ein nichnegativer Term T(x) sein Extremum in xm annimmt, genau dann, wenn das auch für T(x)2 der Fall ist, lässt sich auch grafisch plausibilisieren. Die anspruchsvolle und komplexe händische Lösung ist nicht algorithmisierbar, denn sie führt nur selten bei anderen Extremwertaufgaben zum Erfolg. -Die händische Methode ist wegen des heuristischen Prozesses nicht geeignet, mit einem Computeralgebrawerkzeug ausgeführt zu werden!
Mit der Differenzmethode von Schellbach (1860) verfügt man über eine elementare Methode zur Bestimmung von Extremstellen (falls die Existenz eines Extremen gesichert werden kann). Diese Methode ist algorithmisierbar für rationale Funktionen und solche Funktionen, die durch extremwertstellen-invariante Operationen (wie z.B. durch Quadrieren von nichtnegativen Funktionen) auf rationale Funktionen zurückgeführt. werden können. – Die Differenzgleichheit der Funktionswerte der Schnittpunkte einer horizontalen Sekante mit der Funktionskurve und auch die algebraische Bedeutung der Grenzlage der Sekante sind evident. Das Abarbeiten der Lösung mit DERIVE spart eine Menge an algebraischer Umformungs- und Lösungsarbeit, die bei einem händischen Ausführen der Lösung eher demotivierend wäre. Die Kompetenz zur Benutzung von DERIVE ist aber dafür recht groß, sie ist eigentlich nicht durch einen episodischen Einsatz von DERIVE zu erwerben, sondern sie muss langfristig erworben werden.
Resümee: Um die durch Computerwerkzeuge hervorgerufene Methodenvielfalt zur Geltung zu bringen, müssen die betreffenden Werkzeuge mehr oder weniger gut beherrscht werden. Einerseits kann diese Voraussetzung das gegenwärtige Curriculum schon zeitlich nicht leisten und andererseits kann das Erlernen verschiedener Benutzeroberflächen den Schülern nicht zugemutet werden. Es mangelt also sowohl an einer besseren Integration der Computernutzung in den Mathematikunterricht als auch an der Entwicklung eines geeigneten modularen, multifunktionalen und adaptiven Computerwerkzeugs für den Mathematikunterricht in der Sekundarstufe I, dessen Benutzungskompetenz in einem langfristigen Lernprozess an den auf die Klassenstufen bezogenen mathematischen Themen wachsend angeeignet werden kann.
Unter diesem Aspekt bleiben als eine "optimale" Lösung für die mehrmethodische Behandlung bei entsprechenden Computervoraussetzungen folgende Varianten: Behandlung der speziellen Extremwertaufgaben nach 2.1 "Vom Papiermodell zur Tabellenkalkulation" mit ansschließender händischer Lösung der allgemeinen Extremwertaufgabe nach 2.5 (eine Behandlung mit "minimalen" Computereinsatz).
Eine Behandlung der speziellen Extremwertaufgabe mittels direkter Manipulation auf einem interaktiven Arbeitsblatt nach 2.3 und computerunterstützte Lösung der allgemeinen Extremwertaufgabe nach der Differenzmethode 2.6 (eine Behandlung mit "maximalem" Computereinsatz).
– Aber eigentlich hätten die Schüler und Schülerinnen ein Anrecht, exemplarisch zu erfahren, wie ein mathematischer Unterrichtsgegenstand mit einer Vielfalt an vor allem computerisierten Methoden behandelt werden kann.
4. Literatur
Laborde, J.M.; Bellemain, F. (1996): Cabri Géomètre II. Windows- und DOS-Version 1.0 – Dallas/USA u. Freising: Texas Instruments. (Deutsche Oberfläche und Bearbeitung des Handbuchs von H. Schumann)
Schellbach, K.H. (1860): Mathematische Lehrstunden. Aufgaben aus der Lehre vom Größten und Kleinsten. Berlin: Reimer
Schumann, H. (1994): Schulgeometrisches Konstruieren mit dem Computer. – Velten: Becker
Schumann, H. (1998a): Interaktive Arbeitsblätter für das Geometrielernen. – In: Mathematik in der Schule 36(10), S. 562-569
Schumann, H. (1998b): Geometrische Extremwertaufgaben in dynamischer Behandlung. – In: ZDM Zentralblatt für Didaktik der Mathematik 30(6), S. 215-223
Schumann, H. (1999): Computerunterstütztes Entdecken und Lösen geometrischer Extremwertaufgaben in der Sekundarstufe I. In: Mathematik in der Schule 37(2), S. 110-117
Schumann, H. (1999): Methodenvariation mittels dynamischer Geometrie – exemplarisch. In: ZDM Zentralblatt für Didaktik der Mathematik 31(4), S. 121-132
Autor:
Prof. Dr. habil. Heinz Schumann