Heinz Schumann, PH Weingarten

 

Zur Geschichte präformaler Extremwertbestimmung

Inhalt

Ausgehend von Pierre de Fermat (1601- 1655) wird die Geschichte präformaler Extremwertbestimmung von Funktionen einer reellen Variablen im gymnasialen Unterricht des 19. Jahrhunderts skizziert.

Eine aktuelle didaktische Bewertung dieser Art von Extremwertbe-

stimmung soll unter Berücksichtigung von Computerwerkzeugen für

die Dynamische Geometrie und die Algebra vorgenommen werden.

 

1 Einleitung

2 Zur Geschichte der präformalen Extremwertbestimmung

im 19. Jahrhundert

2.1 Zur Situation des Mathematikunterrichts an den

(preußischen) Gymnasien

2.2 Bedeutende Arbeiten über elementarisierte Extremwert-

bestimmung

2.2.1 Die Methode von Schaffer

2.2.2 Die Methode von Schellbach

2.2.3 Die Methode von Schrader

2.3 Aktualisierung und Ergänzung der Methode von Schellbach

mittels Computereinsatz

3 Schlussbemerkungen

 

Vortrag auf der 5. Tagung der Fachsektion Geschichte der Mathematik

Der Deutschen Mathematiker-Vereinigung

(zugleich 6. Sitzung des Arbeitskreises Mathematikgeschichte und Unterricht

der Gesellschaft für Didaktik der Mathematik

in Bautzen-Schmochtitz (2.6.-6.6. 1999)

Prof.Dr.habil. Heinz Schumann,

Fakultät III, Mathematik/Informatik u. Institut für Bildungsinformatik

PH Weingarten, Kirchplatz 2, D-88250 Weingarten

Email: Schumann@PH-Weingarten.De

Vortragsfolien (Auswahl):

Zur Erfindung der Differentialrechnung haben hauptsächlich

drei Fragestellungen Anstoß gegeben:

(d. h. die Frage nach der Ermittlung der Tangente in einem Punkt einer "krummen Linie")

(d. h. die Frage nach der Berechnung der Geschwindigkeit eines sich auf einer Bahn bewegenden Punktes in einem bestimmten Moment)

(d. h. die Frage nach der Bestimmung des Maximums und Minimums einer Funktion)

 

 

 

 

 

 

 

 

 

 

 

Leibnizsche Theorie der relativen Extrema

Gottfried Wilhelm Leibniz (1646 - 1716):

"Nova methodus pro maximis et minimis itemque tangentibus" (1684)

 

SATZ(Leibniz, 1684)*: Notwendig dafür, dass die in [a,b] stetige und in ]a,b[ differenzierbare Funktion x ® f(x) an der Stelle x0]a,b[ ein relatives Extremum besitzt, ist die Bedingung

f '(x0) = 0.

Das Schaubild der Funktion x ® f(x) muß also an einer Stelle x0]a,b[, die ein solches relatives Extremum von f(x) ergeben soll, notwendig eine horizontale Tangente besitzen.

SATZ (Leibniz, 1684): Hinreichend dafür, dass die in [a,b] stetige Funktion x ® f (x), die in ]a,b[ differenzierbar ist und an der Stelle x0]a,b[ eine zweite Ableitung f ''(x0) besitzt, an der Stelle x0 ein eigentliches

relatives Minimum

relatives Maximum

besitzt, sind die Bedingungen:

f '(x0) = 0, f ''(x0) > 0

f '(x0) = 0, f ''(x0) < 0.

 

 

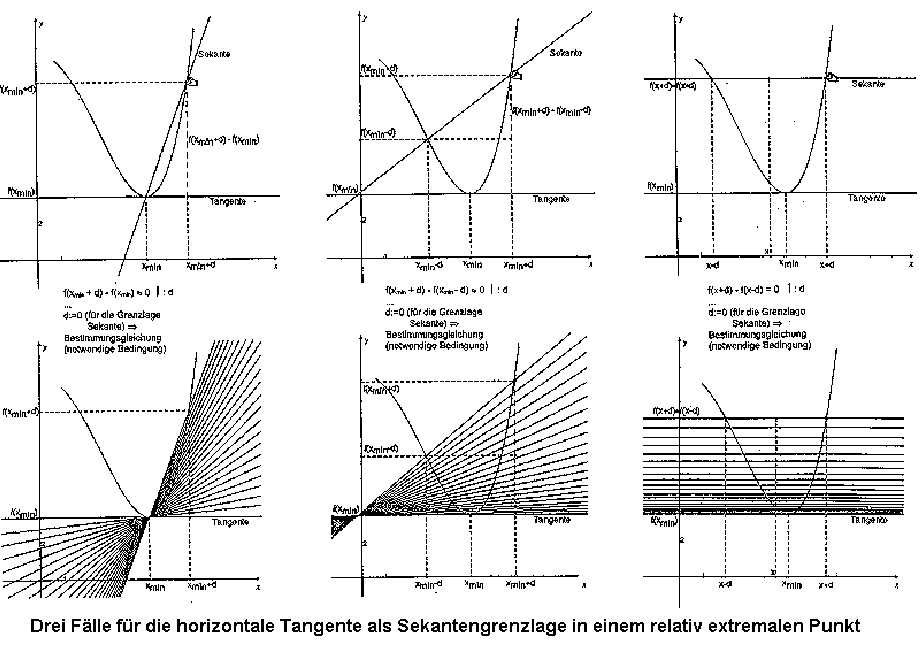
Präformale Extremwertbestimmung

Eine Extremwertbestimmung von reellen Funktionen soll

präformal bzw. elementarisiert genannt werden, wenn sie

nicht die Leibnizsche Theorie der Extrema benutzt

und den Grenzwertbegriff nur implizit verwendet.

 

___________

* in der heutigen Schreibweise nach Lagrange (1736-1813)

Arbeiten über präformale bzw. elementarisierte Extremwertbestimmung:

 

Schaffer, J.F.: Geometrische Aufgaben mit vollständigen

Auflösungen zum Selbstunterricht für An-

Fänger. Oldenburg 1816

Schellbach, K.H.: Mathematische Lehrstunden.

Aufgaben aus der Lehre

vom Größten und Kleinsten. Berlin 1860

Martus, H.C.E.: Maxima und Minima.

Ein geometrisches und algebraisches

Übungsbuch für die Schüler höherer

Lehranstalten. Berlin 1861

Schrader, W.: Neue allgemeine Methode zur elementaren

Bestimmung des Maximums und Minimums.

Halle 1862

Förster, C.: Darstellung der elementaren Theorie der Maxima

und Minima und ihre Anwendung.

In: Programm der Domschule zu Güstrow.

Ausgegeben Ostern 1866. S. 1-32b

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Karl Heinrich Schellbach (1804 - 1892)

 

kann als einer der führenden deutschen "Mathematikdidaktiker"

In der Mitte des 19. Jahrhunderts bezeichnet werden.

 

Er gründete das erste Institut zur Ausbildung gymnasialer Mathematik-

u. Physiklehrer ("Schellbachsches Seminar", Berlin 1855)

Mit seiner Denkschrift "Vorschläge zu einer Reform des mathemati-schen und physikalischen Unterrichts an unseren Gymnasien" (1860) gab er wesentliche Impulse für die Mathematik- u. Physiklehreraus-bildung.

Als Autor vor allem methodisch-didaktischer Arbeiten u. Werke über

Themen der Analysis und der Angewandten Mathematik nahm er Ein-fluß auf die Gestaltung des Mathematikunterricht an Gymnasien und Realschulen.

Als Mitherausgeber des "Crelleschen Journals" (ab 1855) und als

Gesprächspartner berühmter zeigenössischer Mathematiker förderte

er die wissenschaftliche Kommunikation.

 

 

Literatur:

Müller, F.: Karl Schellbach. Rückblick auf sein wissenschaftliches

Leben. Leipzig 1905

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Schellbach, S.17

 

 

 

 

 

 

 

 

 

 

Schellbach, S.17/18

Schellbach, S. 18

Schellbach, S.24/25

 

Müller, Seite 106

 

 

 

 

 

 

 

 

Müller, S.108/109

 

 

Experimentelle Methode

zur Entdeckung und näherungsweisen Lösung

von Extremwertaufgaben mittels dynamischer Geometrie

(Schumann 1998)

 

  1. Konstruktion einer geometrischen Figur, die auch Nebenbedingungen erfüllt

  2. Variation einer unabhängigen Größe der Figur bzw. Teilfigur unter Beobachtung eines funktionalen Zusammenhangs: unabhängige Größe - abhängige Größen (Datensammlung in Werte-Tabelle; grafische Darstellung im Schaubild)

  3. Erkennen einer extremalen Eigenschaft (näherungsweises Bestimmen von Extremstelle und Extremwert)

  4. Variation der Figurenparameter und Prüfung, ob extremale Eigenschaft invariant

(5) Formulierung einer geometrischen Extremwertaufgabe als (allgemeine)

Berechnungsaufgabe.

 

 

 

 

 

 

 

 

 

 

 

 

 

Elementarisierte Methode zur Berechnung von relativen Extrema*

(nach Schellbach 1860)

  1. Aufstellen der Zielfunktion mit dem Funktionsterm f(x)

    2. (auch unter Berücksichtigung einer Nebenbedingung)

  2. Gleichung f(x + d) - f(x - d) = 0 bilden

(3) Ausklammern von d und Nullsetzen des wesentlichen Faktors

(4) Gewinnen der Bestimmungsgleichung für xm: d gleich Null setzen

(5) Exaktes (oder näherungsweises) Lösen der Bestimmungsgleichung

(6) Berechnen des Extremwertes durch Einsetzen von xm in f (x)

(Prüfung zulässiger Lösungen im Aufgabenkontext)

(7) Berechnen weiterer gesuchter Größen

______

* im wesentlichen für rationale Funktionen

Computerisierte Lösung der "Schellbach-Aufgabe" Nr. 20 (modifiziert):

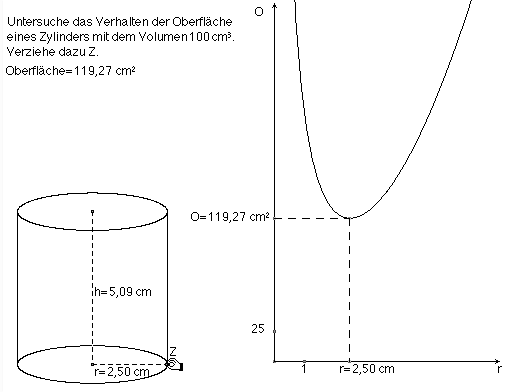
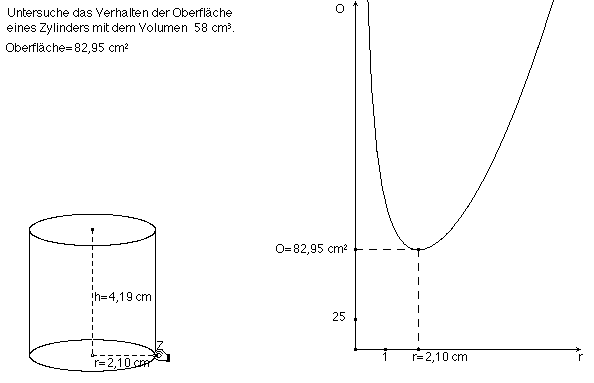
... mit dynamischer CABRI-Geometrie

 

 

 

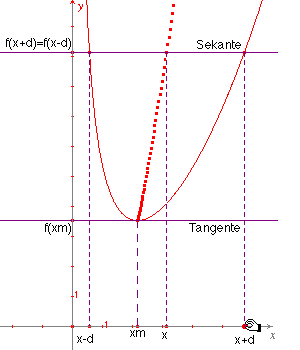
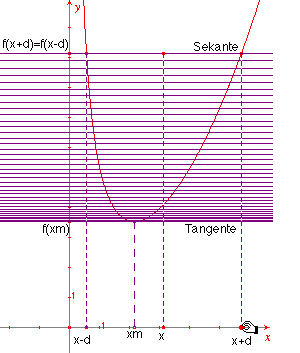
Schellbach dynamisch ...

 



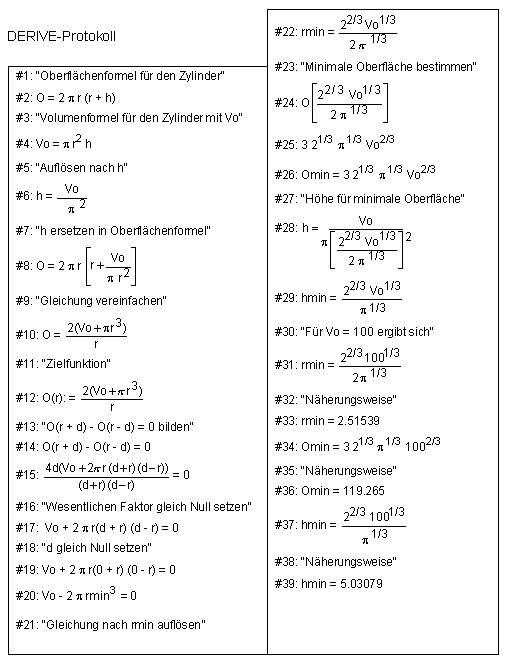
© 1999 by Heinz Schumann, Zur Geschichte präformaler Extremwertbestimmung, ISSN 0932-2736

Titelseite

Inhaltsangabe

Geometrische Extremwertaufgaben in dynamischer Behandlung

Computerunterstütztes Entdecken und Lösen geometrischer Extremwertaufgaben in der Sekundarstufe I

Methodenvariation mittels dynamischer Geometrie am Beispiel umfangs- und flächengleicher Rechtecke

Medienspezifische Methodenvielfalt bei der Behandlung einer Extremwertaufgabe

Zur Geschichte präformaler Extremwertbestimmung (Vortragsfolien)

Endseite

ml;ngig von der Radiusgröße ein Sektor mit diesem Winkel herausgeschnitten werden, um den optimalen Kugelmantel zu erhalten.)